Bài viết này hướng dẫn chi tiết cách Soạn Bài Toán Lớp 9 Tập 2 Bài 10 về vị trí tương đối của hai đường tròn. Chúng ta sẽ cùng nhau khám phá các trường hợp giao nhau, tiếp xúc và không giao nhau của hai đường tròn, cùng với cách giải các bài tập liên quan.

Tìm Hiểu Về Vị Trí Tương Đối Của Hai Đường Tròn

Vị trí tương đối của hai đường tròn được xác định bởi khoảng cách giữa tâm của chúng và tổng/hiệu bán kính. Có ba vị trí tương đối chính:

• Hai đường tròn cắt nhau: Khi khoảng cách giữa hai tâm nhỏ hơn tổng bán kính và lớn hơn hiệu bán kính. Hai đường tròn có hai điểm chung.
• Hai đường tròn tiếp xúc nhau: Khi khoảng cách giữa hai tâm bằng tổng bán kính (tiếp xúc ngoài) hoặc bằng hiệu bán kính (tiếp xúc trong). Hai đường tròn có một điểm chung.
• Hai đường tròn không giao nhau: Khi khoảng cách giữa hai tâm lớn hơn tổng bán kính (không giao nhau ngoài) hoặc nhỏ hơn hiệu bán kính (đường tròn nằm trong đường tròn). Hai đường tròn không có điểm chung.

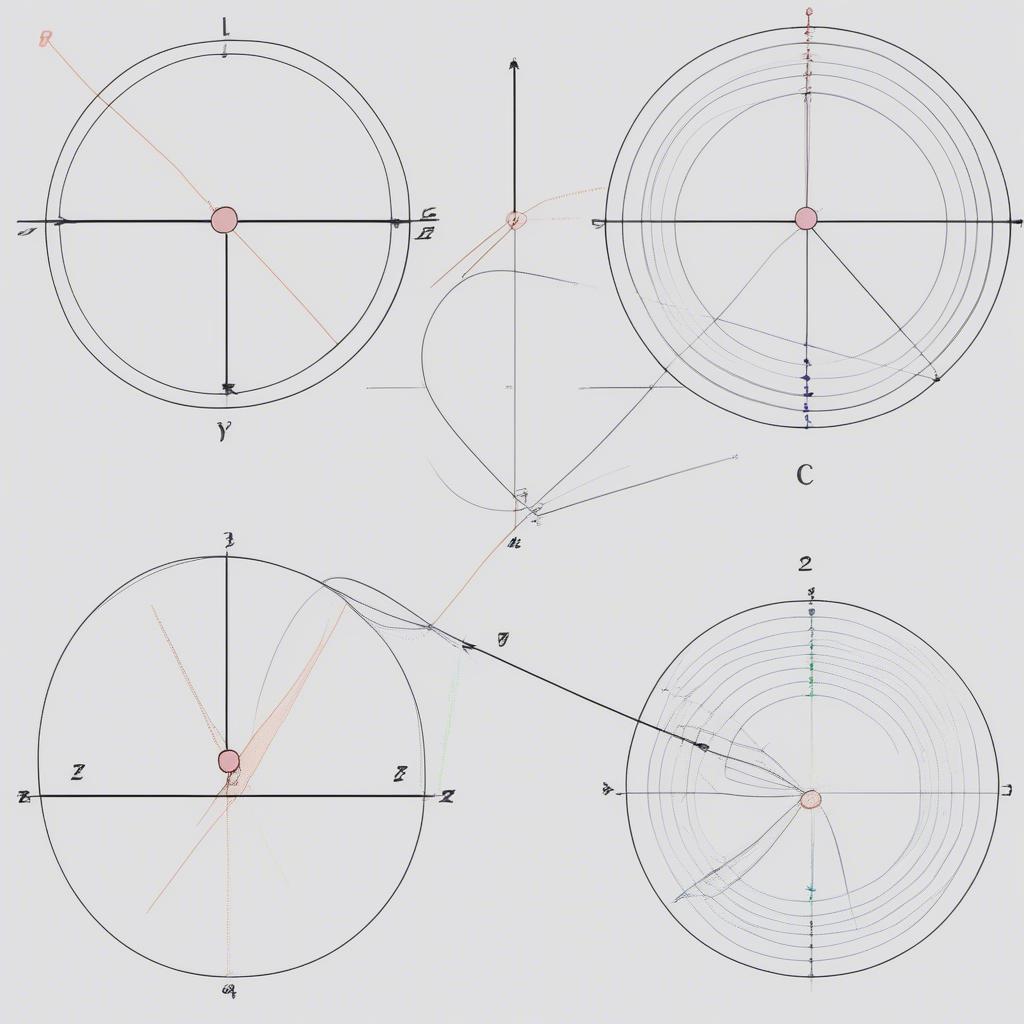Vị trí tương đối của hai đường tròn

Cách Xác Định Vị Trí Tương Đối Của Hai Đường Tròn

Để xác định vị trí tương đối của hai đường tròn (O; R) và (O’; r) với R ≥ r, ta tính khoảng cách OO’ giữa hai tâm và so sánh với tổng và hiệu bán kính:

1. OO’ > R + r: Hai đường tròn không giao nhau (ngoài).
2. OO’ = R + r: Hai đường tròn tiếp xúc ngoài.
3. R – r < OO’ < R + r: Hai đường tròn cắt nhau.
4. OO’ = R – r: Hai đường tròn tiếp xúc trong.
5. OO’ < R – r: Đường tròn (O’; r) nằm trong đường tròn (O; R).

Cách xác định vị trí tương đối của hai đường tròn

Bạn đang tìm kiếm tài liệu ôn tập cho kỳ thi sắp tới? Hãy tham khảo toán hình lớp 10 ôn tập chương 1.

Bài Tập Vận Dụng

Xét hai đường tròn (O; 5cm) và (O’; 3cm) với OO’ = 8cm. Vì OO’ = 8cm > R + r = 5cm + 3cm = 8cm, nên hai đường tròn tiếp xúc ngoài.

Nếu OO’ = 2cm thì vì OO’ = 2cm < R – r = 5cm – 3cm = 2cm, nên đường tròn (O’; 3cm) nằm trong đường tròn (O; 5cm).

Bạn muốn tìm hiểu thêm về các đề thi toán? Tham khảo đề thi vào 10 môn toán hồ chí minh.

Mẹo Học Tập Hiệu Quả

• Vẽ hình minh họa để dễ dàng hình dung vị trí tương đối của hai đường tròn.
• Ghi nhớ các công thức tính khoảng cách và so sánh bán kính.
• Luyện tập nhiều bài tập để nắm vững kiến thức.

Mẹo học tập hiệu quả

Bạn muốn thử sức với các đề thi chuyên? Xem ngay đề thi chuyên toán lớp 10 quốc gia hà nội.

Kết Luận

Soạn bài toán lớp 9 tập 2 bài 10 giúp học sinh hiểu rõ về vị trí tương đối của hai đường tròn. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học toán hình ở các lớp cao hơn.

FAQ

1. Làm thế nào để phân biệt tiếp xúc trong và tiếp xúc ngoài?
2. Khi nào hai đường tròn cắt nhau?
3. Khi nào một đường tròn nằm trong đường tròn khác?
4. Khoảng cách giữa hai tâm có ý nghĩa gì trong việc xác định vị trí tương đối?
5. Làm thế nào để tính khoảng cách giữa hai tâm đường tròn?
6. Có bao nhiêu vị trí tương đối của hai đường tròn?
7. Làm sao để nhớ các trường hợp vị trí tương đối của hai đường tròn?

Mô tả các tình huống thường gặp câu hỏi.

Học sinh thường gặp khó khăn khi phân biệt tiếp xúc trong và tiếp xúc ngoài, cũng như khi xác định vị trí tương đối khi khoảng cách giữa hai tâm bằng hiệu bán kính. Việc luyện tập nhiều bài tập với các hình vẽ minh họa sẽ giúp khắc phục những khó khăn này.

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tìm hiểu thêm về các bài toán liên quan đến đường tròn tại tài liệu giáo khoa chuyên toán đại số 10 hoặc làm bài tập trong đề thi toán tuyển sinh lớp 10 phú yên 2019.