Hệ số góc của đường thẳng là một khái niệm quan trọng trong chương trình Toán lớp 10. Nắm vững khái niệm này sẽ giúp bạn giải quyết nhiều bài toán liên quan đến đường thẳng một cách hiệu quả. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về hệ số góc, từ định nghĩa, cách tính, ý nghĩa hình học đến ứng dụng trong các bài toán thực tế.

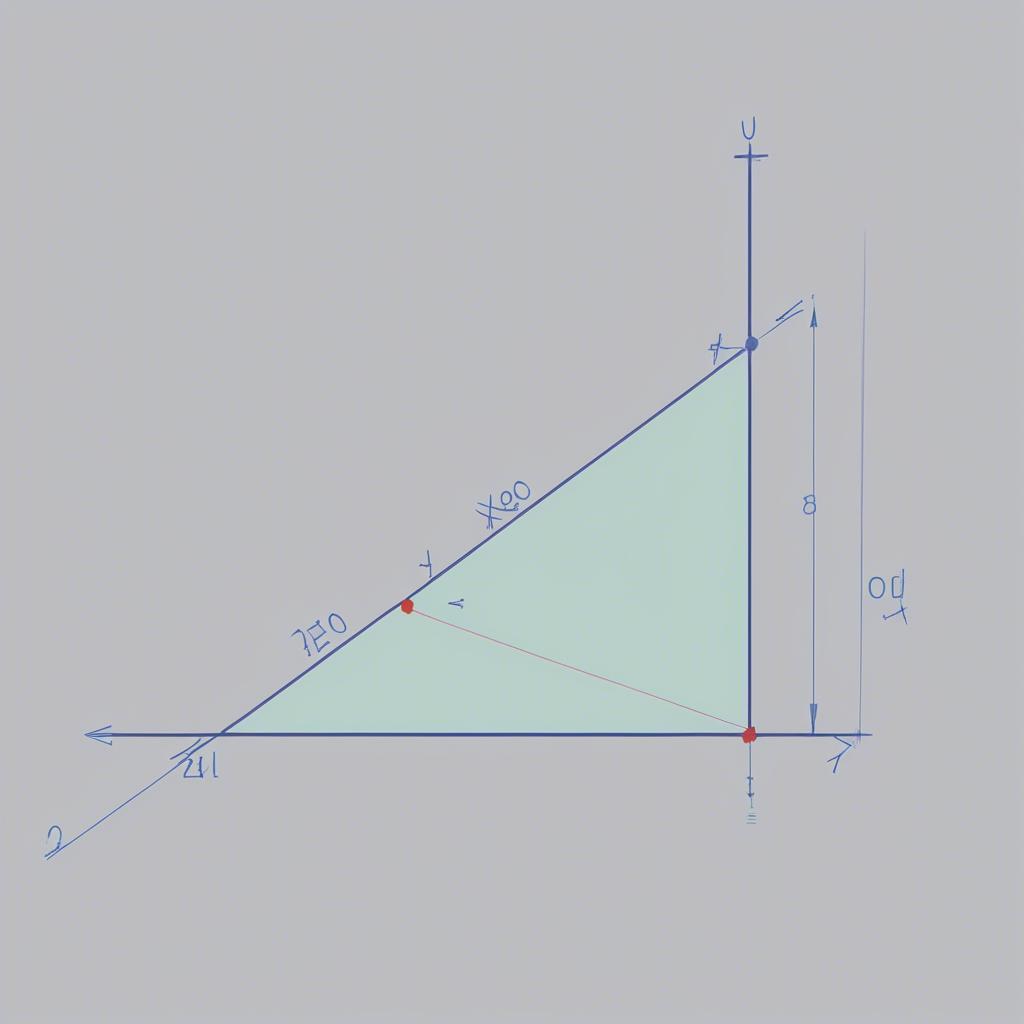Hệ số góc của đường thẳng trong hình học tọa độ lớp 10

Định Nghĩa Hệ Số Góc Của Đường Thẳng

Hệ số góc của một đường thẳng không thẳng đứng trong mặt phẳng tọa độ Oxy, thường được ký hiệu là k, được định nghĩa là tang của góc tạo bởi đường thẳng đó với chiều dương của trục Ox. Nói cách khác, nếu góc giữa đường thẳng và trục Ox là α thì k = tan(α).

Đối với đường thẳng thẳng đứng, hệ số góc không xác định. Đường thẳng nằm ngang (song song với trục Ox) có hệ số góc bằng 0.

Sau khi tìm hiểu định nghĩa, hãy cùng xem cách tính toán hệ số góc. công thức toán lớp 10 ku2 2 có thể giúp bạn làm quen với một số công thức liên quan.

Cách Tính Hệ Số Góc

Có nhiều cách để tính hệ số góc của một đường thẳng. Dưới đây là hai cách phổ biến nhất:

• Qua hai điểm: Nếu biết tọa độ hai điểm A(x₁, y₁) và B(x₂, y₂) nằm trên đường thẳng, hệ số góc được tính bằng công thức: k = (y₂ – y₁) / (x₂ – x₁).

• Qua phương trình đường thẳng: Nếu phương trình đường thẳng được viết dưới dạng y = ax + b, thì hệ số góc chính là hệ số a.

Ví dụ minh họa cách tính hệ số góc của đường thẳng

Ý Nghĩa Hình Học Của Hệ Số Góc

Hệ số góc thể hiện độ dốc của đường thẳng. Giá trị tuyệt đối của hệ số góc càng lớn, đường thẳng càng dốc. Dấu của hệ số góc cho biết đường thẳng hướng lên hay hướng xuống. Nếu k > 0, đường thẳng hướng lên. Nếu k < 0, đường thẳng hướng xuống.

Hệ Số Góc Và Vị Trí Tương Đối Của Hai Đường Thẳng

Hệ số góc giúp xác định vị trí tương đối của hai đường thẳng. Hai đường thẳng song song có cùng hệ số góc. Hai đường thẳng vuông góc có tích hệ số góc bằng -1. Bạn có thể tìm hiểu thêm về 2 đường thẳng vuông góc toán 10.

Giáo sư Nguyễn Văn A, chuyên gia Toán học tại Đại học Sư Phạm Hà Nội, chia sẻ: “Hiểu rõ về hệ số góc là chìa khóa để giải quyết nhiều bài toán hình học phẳng, đặc biệt là các bài toán liên quan đến đường thẳng.”

Ứng Dụng Của Hệ Số Góc Trong Bài Toán Thực Tế

Hệ số góc có nhiều ứng dụng trong thực tế, ví dụ như trong vật lý để tính vận tốc, gia tốc, trong kinh tế để tính tốc độ tăng trưởng…

Ứng dụng hệ số góc trong bài toán thực tế

Kết luận

Hệ Số Góc Của đường Thẳng Toán 10 là một khái niệm cơ bản nhưng vô cùng quan trọng. Hiểu rõ về hệ số góc sẽ giúp bạn giải quyết nhiều bài toán liên quan đến đường thẳng một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về hệ số góc. dđề kiểm tra một tiết toán lớp 10 kì 2 có thể giúp bạn ôn tập và củng cố kiến thức.

FAQ

1. Hệ số góc của đường thẳng là gì?
2. Làm thế nào để tính hệ số góc của đường thẳng?
3. Ý nghĩa hình học của hệ số góc là gì?
4. Hệ số góc có ứng dụng gì trong thực tế?
5. Làm thế nào để xác định vị trí tương đối của hai đường thẳng bằng hệ số góc?
6. Hệ số góc của đường thẳng song song với trục Ox là bao nhiêu?
7. Hệ số góc của đường thẳng vuông góc với trục Ox là bao nhiêu?

Mô tả các tình huống thường gặp câu hỏi.

Học sinh thường gặp khó khăn khi tính hệ số góc của đường thẳng trong các trường hợp đặc biệt như đường thẳng thẳng đứng hoặc nằm ngang. Cần lưu ý rằng đường thẳng thẳng đứng không có hệ số góc, còn đường thẳng nằm ngang có hệ số góc bằng 0.

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tham khảo thêm toán lớp 7 bài 8 trang 10 hoặc bt toán 8 bài 10 để củng cố kiến thức về đường thẳng.