

Cách Xét Dấu Trong Toán Lớp 10 là một trong những kiến thức nền tảng quan trọng, giúp học sinh giải quyết nhiều bài toán liên quan đến bất phương trình, phương trình và các dạng bài tập khác. Nắm vững cách xét dấu sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán phức tạp. luyện thi vào 10 môn toán thanh hóa
Tại Sao Việc Xét Dấu Lại Quan Trọng Trong Toán Học?
Xét dấu của một biểu thức toán học giúp chúng ta xác định được khoảng giá trị của biến số làm cho biểu thức đó mang dấu dương, dấu âm hoặc bằng 0. Điều này cực kỳ hữu ích trong việc giải quyết bất phương trình, tìm nghiệm của phương trình, và vẽ đồ thị hàm số.
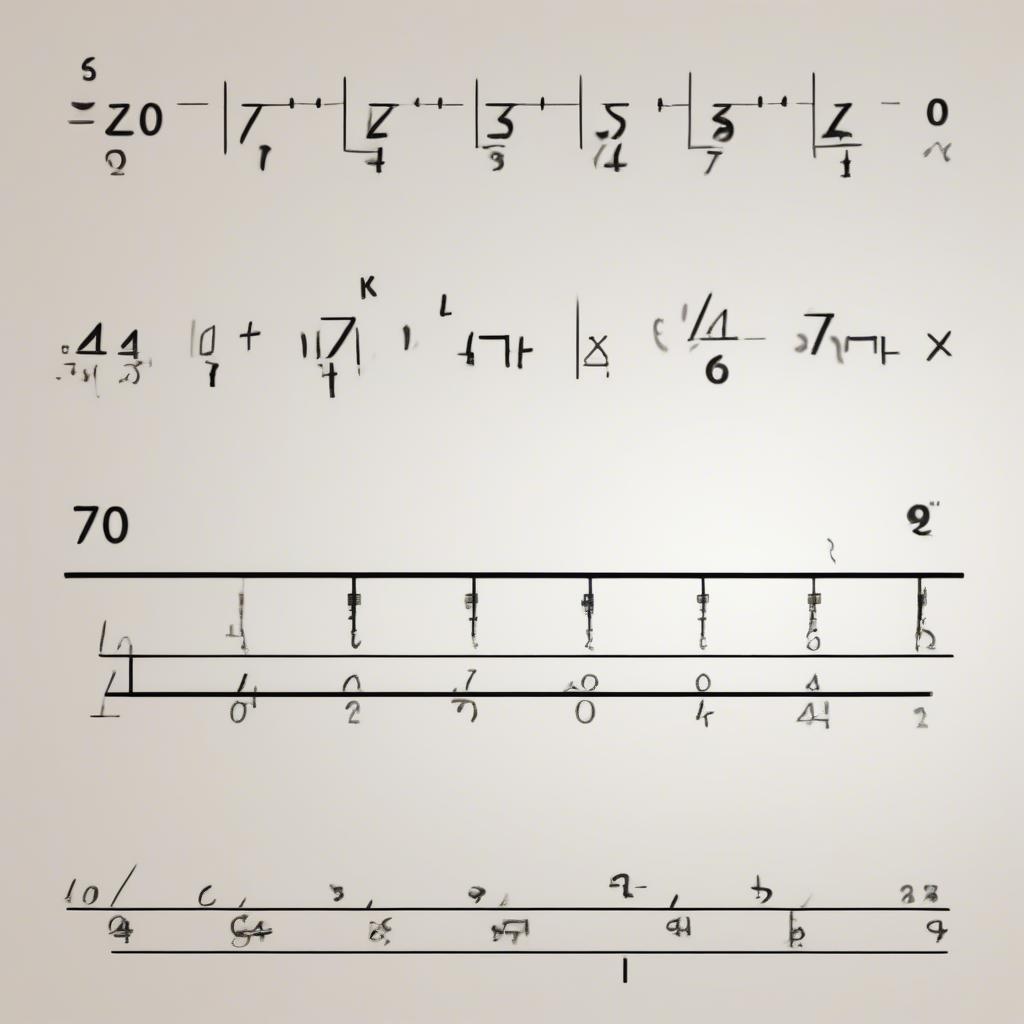 Xét dấu bằng xét dấu
Xét dấu bằng xét dấu
Các Phương Pháp Xét Dấu Thường Gặp Trong Toán Lớp 10
Phương Pháp Xét Dấu Bằng Bảng Xét Dấu
Đây là phương pháp phổ biến và dễ hiểu nhất. Chúng ta sẽ lập một bảng xét dấu, bao gồm các nghiệm của biểu thức và các khoảng giá trị của biến. Sau đó, dựa vào quy tắc xét dấu của từng thừa số, ta xác định dấu của biểu thức trên từng khoảng.
Xét Dấu Bằng Cách Sử Dụng Đường Parabol (Đối Với Tam Thức Bậc Hai)
Đối với tam thức bậc hai dạng ax² + bx + c, ta có thể xét dấu bằng cách vẽ đường parabol y = ax² + bx + c. Dựa vào vị trí của parabol so với trục hoành, ta xác định được khoảng giá trị của x làm cho tam thức bậc hai dương, âm hoặc bằng 0.
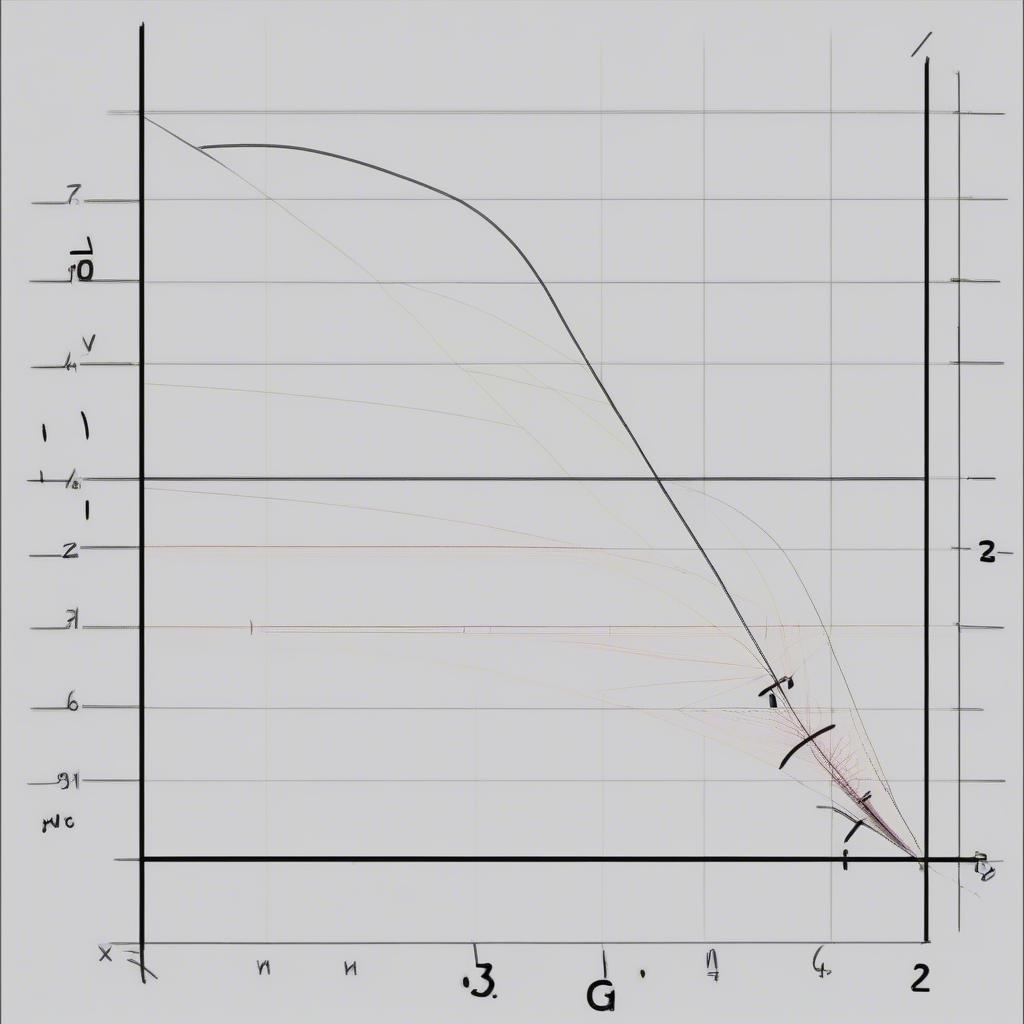 Xét dấu bằng đường parabol
Xét dấu bằng đường parabol
Ví Dụ Minh Họa Cách Xét Dấu
Ví dụ 1: Xét dấu của biểu thức f(x) = (x-1)(x+2)
Ta lập bảng xét dấu như sau:
| x | -∞ | -2 | 1 | +∞ |
|---|---|---|---|---|
| x-1 | – | – | 0 | + |
| x+2 | – | 0 | + | + |
| f(x) | + | 0 | – | + |
Vậy f(x) > 0 khi x < -2 hoặc x > 1; f(x) < 0 khi -2 < x < 1; f(x) = 0 khi x = -2 hoặc x = 1.
Ví dụ 2: Xét dấu của tam thức bậc hai f(x) = x² – x – 2
Ta có thể phân tích tam thức bậc hai thành nhân tử: f(x) = (x-2)(x+1). Sau đó, ta lập bảng xét dấu tương tự như Ví dụ 1. Hoặc, ta có thể vẽ parabol y = x² – x – 2 và dựa vào vị trí của parabol so với trục hoành để xét dấu. sách toán 10 nâng cao hay
Mẹo Học Tập Hiệu Quả Về Xét Dấu
- Nắm vững quy tắc xét dấu: Ghi nhớ quy tắc xét dấu của các biểu thức cơ bản như (x-a), (x+a), ax² + bx + c.
- Luyện tập thường xuyên: Giải nhiều bài tập để thành thạo kỹ năng xét dấu.
- Sử dụng công cụ hỗ trợ: Có thể sử dụng phần mềm vẽ đồ thị để kiểm tra kết quả xét dấu. cậu hỏi toán học 10 phương trình
 Luyện tập xét dấu
Luyện tập xét dấu
Kết luận
Cách xét dấu trong toán lớp 10 là một kiến thức quan trọng và cần thiết. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích về cách xét dấu, giúp bạn tự tin hơn trong việc giải quyết các bài toán. bài tập cơ bản toán đại 10 chương 3
FAQ
- Khi nào nên sử dụng bảng xét dấu?
- Khi nào nên sử dụng đường parabol để xét dấu?
- Làm thế nào để nhớ quy tắc xét dấu?
- Có những phần mềm nào hỗ trợ việc xét dấu?
- Xét dấu có ứng dụng gì trong thực tế?
- Xét dấu có liên quan gì đến việc giải bất phương trình?
- Làm sao để phân biệt được các khoảng nghiệm khi xét dấu?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn khi xét dấu các biểu thức phức tạp, chứa nhiều nhân tử hoặc chứa căn thức. Việc xác định đúng dấu của từng nhân tử và kết hợp chúng lại để tìm ra dấu của toàn bộ biểu thức là một thách thức đối với nhiều học sinh. de thi toán lớp 10 đà nẵng 2017
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài toán liên quan đến bất phương trình, phương trình bậc hai và các chủ đề khác trên website Đại CHiến 2.




